|
Na
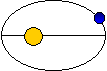
Folha anterior referiu-se que a Terra se move à
volta do Sol com uma órbita elíptica. Acerca dessa
elipse, informou-se que:
- O Sol ocupa um dos focos;
-
O eixo maior mede 14957000 km;
-
A distância focal é 249782 km. |
a)
Quanto
mede o eixo menor da elipse?
|
Utilizando
a notação habitual, tem-se:
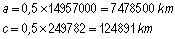
|
|
|
Logo,
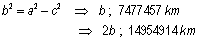
O
eixo maior mede cerca de 14954194 km.
|
b)
A que distância fica a Terra do Sol no Solstício de
Verão?
O
Solstício de Verão (21 de Junho) corresponde ao dia em
que a Terra está mais distante do Sol. Nesse dia a distância
da Terra ao Sol é
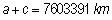
| a)
Qual é o lugar geométrico da pastagem comum? |
|
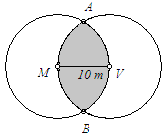
O
conjunto dos pontos correspondente a intersecção
de dois círculos de raio 10 m e cujos centros
distam 10 m.
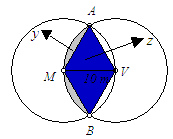
Na
figura, M e V representam os pontos em que estão as
estacas a que estão presas a Mimosa e a Vigor,
respectivamente.
|
|
| b)
Quanto mede a área da pastagem comum?
|
|
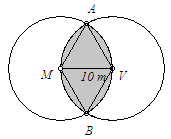 |
O
triângulo [AMV] é equilátero, porque |
|
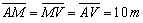
|
| Então, |
|
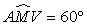
|
|
Da
mesma forma se conclui que o triângulo [BMV] é
equilátero. |
| Logo, |
|
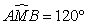
|
|
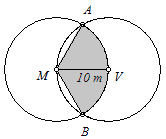
Notemos
por x
a área da parte sombreada na figura ao lado. |
 |
|
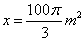
|
| Notando
por y
e z
as regiões assinaladas na figura abaixo, |
|
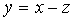
|
 |
Determinação
de z:
|
|
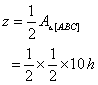
|
| em
que |
|
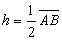 |
| Aplicando
o Teorema de Pitágoras:
|
|
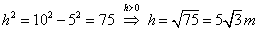
|
| Então, |
|
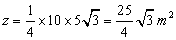
|
| Logo, |
|
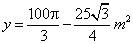
|
| Então,
a área da região resultante da intersecção dos
dois círculos é |
|
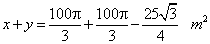
|
| R:
A área de pastagem comum mede |
|
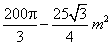
|
|
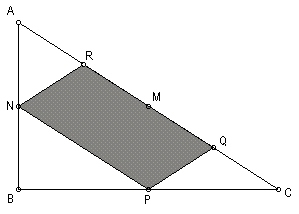
Como
M, R e Q são os pontos médios de [AB], [AM] e [BM],
respectivamente, então |
 |
|
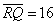
|
|
Os
triângulos [ABC] e [NCP]
são semelhantes, porque têm um ângulo
comum e os lados correspondentes proporcionais: |
|
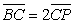
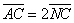
|
| Então
o perímetro de [NPQR] é 48. |
|