|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
2 |
4 |
6 |
8 |
10 |
12 |
14 |
16 |
18 |
|
3 |
6 |
9 |
12 |
15 |
18 |
21 |
24 |
27 |
|
4 |
8 |
12 |
16 |
20 |
24 |
28 |
32 |
36 |
|
5 |
10 |
15 |
20 |
25 |
30 |
35 |
40 |
45 |
|
6 |
12 |
18 |
24 |
30 |
36 |
42 |
48 |
54 |
|
7 |
14 |
21 |
28 |
35 |
42 |
49 |
56 |
63 |
|
8 |
16 |
24 |
32 |
40 |
48 |
56 |
64 |
72 |
|
9 |
18 |
27 |
36 |
45 |
54 |
63 |
72 |
81 |
 |
Estas «mal alinhavadas regras», como
soe dizer-se a propósito de tantas coisas, têm, como todas as
outras, a sua razão de ser: este ano... da graça de 1951, em
plenos exames de admissão, como faço sempre que posso, tentei,
mais uma vez, verificar até que ponto os alunos — candidatos à
matrícula no primeiro ano — eram capazes de utilizar, na
Matemática, que é fundamental, o cálculo em vez do giz. E, como
cada problema que ponho a cada criança é sempre um teste, e não
uma série de contas, com factores de palmo e meio, como, às vezes,
vejo fazer e oiço dizer que se faz, tentei, num dia em que a
assistência, sobretudo de professores, era maior, demonstrar que
aquilo que eu pedia era absolutamente acessível a qualquer cérebro
de DEZ ANOS. A criança — menina — com quem fiz a experiência,
vinha das provas escritas apenas com suficientes, o que me não
dava o direito, nem a ninguém, de a considerar inteligente. Antes
pelo contrário. |
Propus-lhe
multiplicar, salvo erro, 12 por 15.
Não o fez.
Tentei outros dois factores. O mesmo resultado. Perguntei-lhe, então:
mas queres aprender isto, num instante? Resposta pronta «quero».
Ensinei a
primeira vez. Tentei a segunda. Exemplifiquei uma terceira; e, à
quarta, disse-lhe: faz tu agora. Executou 1, 2, 3... 4 exercícios do
mesmo género, mentalmente, com rapidez. Nesta altura, não me tive que
me não voltasse para a assistência; particularmente professores, e não
dissesse: vêem os Senhores que isto é simples?
Ninguém
deixou de perceber. Muitos gostaram, e alguns me perguntaram, no fim
dos exames: mas onde ver isto tudo? Aqui o têm.
Claro que
não é uma coisa perfeita, nem completa, que cada um pode arranjar a
mesma coisa, tão simples quanto lhe parecer, tanto mais que isto foi,
pode dizer-se, feito sobre o joelho. Só tem uma coisa que vale, esta
colecçãozinha de regras: a intenção... e a pretensão de querer ser
claro e simples.
Aveiro,
1952.
Na adição
ADIÇÃO DE 2 OU MAIS
NÚMEROS, DE DEZENAS, CENTENAS, MILHARES, ETC.
Para a
realizarmos, mentalmente, basta juntar as unidades da mesma espécie, e
acrescentar à soma igual n.º de zeros.
Assim:
50+80+90=
(5+8+9) 10 =22x10 = 220;
700+900+600=
(7+9+6) 100 = 22x100 = 2200;
2000+3000+5000= (2+3+5) 1000 = 10x1000 = 10000, e assim
sucessivamente.
ADIÇÃO DE DOIS N.ºs
QUAISQUER, INTEIROS
Executa-se
facilmente, decompondo um deles. Exemplos:
925+42 =
925+40+2 = 965+2 = 967;
3428+122 =
3428+100+20+2 = 3528+20+2 = 3548+2 = 3550;
5876+924 =
5876+900+20+4 = 6776 +20 + 4 = 6796+4 = 6800;
ADIÇÃO DE UM N.º
INTEIRO COM OUTRO DECIMAL
Para isso,
procede-se identicamente.
Assim:
723+0,45=723,45
952+0,012=952,012.
ADIÇÃO DE DOIS OU
MAIS N.ºS DECIMAIS
Procede-se
como se fossem inteiros, tendo, no fim, o cuidado de dividi-lo pelo
maior n.º de casas decimais.
Exemplos:
0,48+0,034 = (480+30+4):1000 = (510+4):1000=514:1000=0,514
ADIÇÃO DE VÁRIOS
NÚMEROS
Decompõem-se
os mais pequenos, e procede-se de igual forma.
Assim:
624+38+95=624+30+90+8+5=624+120+13-:-744+13=757;
7200+85+341=7200+300+80+40+5+1=7500+120+6=7620+6=7626;
628+142+0,45
= 628+100+40+2+0,45=728+42+0,45=770+0,45=770,45.
Na subtracção
Se dois
números são compostos só por dezenas, centenas, milhares, etc.,
procede-se, na subtracção mental, da maneira inversa do da soma.
Exemplos: 90-20=(9-2) 10=70;
800-500= (8-5) 100=300;
16000-7000= (16-7) 1000=9000.
No caso de se tratar de 2 n.ºs quaisquer,
é fácil, se se proceder ao invés da soma.
Assim: 945-120=945-20-100=925-100=825;
7973 - 342=7973-2-40- 300=7971-40-300=7931-300=7631
Na multiplicação
MULTIPLICAÇÃO POR 10, 100, 1000, ETC.
Para multiplicar um número inteiro, por
10, 100, 1000, 10000 etc. basta acrescentar-lhe 1, 2, 3, 4 zeros.
Assim:
45x10=450; 3525x100=352500;
170x1000=170000, etc.
Se o número for decimal, basta, para o
multiplicar por 10, 100, etc. andar com a vírgula, 1, 2, 3 casas
decimais (tantas quanto o número de zeros).
Exemplos: 4,2 xl00=420; 3,453x1000=3453, etc., etc.
MULTIPLICAÇÃO POR 11
Multiplica-se um número qualquer por 11,
escrevendo, à direita do multiplicando, o seu 1.º algarismo da
direita, a seguir a soma deste com o seguinte, ou seja com o segundo,
depois a soma do segundo com o terceiro, do terceiro com o quarto, e
assim por diante.
Suponhamos o produto de 728x11=8008, ou
seja 8; 8+2; 1+2+7; 1+7
Do
mesmo modo 7275x11=80025.
MULTIPLICAÇÃO POR 111
Suponhamos 624x111=69264
Como se procedeu? Da mesma maneira que
quando se multiplicou por 11.
Simplesmente, na multiplicação por 111,
cada um dos algarismos do mu1tiplicando, em vez de entrar, no produto,
2 vezes, entrará 3.
Teremos, pois:
4;
4+2; 4+2+6; 1+2+6; 6, ou seja 69264
Multiplicação por 22, 33, 44, 55, 66, 77, 88, 99 ou por 222, 333, 444,
555, 666, 777, 888, 999.
Sabido, como é, que 2x11=22; 3x11=33 e que
2x111=222; 3x111=333, etc., etc. fácil é executar, mentalmente,
qualquer destes produtos. Exemplifiquemos:
956x55=956x5x11=4780x11=52580;
3225x333=3225x3x111=9675x111=1.073.925.
Da
mesma maneira se operará se, em vez de se multiplicar qualquer número
por 111, se multiplicar por 1111, 11111, etc, ou por 3333, 44444, etc.
MULTIPLICAÇÃO DE UM
NÚMERO POR 12, 13, 14, 15, ETC. ATÉ 20
Se os 2 factores são, ambos, inferiores a
20, procede-se da seguinte maneira, rapidamente: a um deles, juntam-se
as unidades do outro, multiplica-se esta soma por 10 e junta-se, a
este produto, o produto das unidades dos dois. Assim:
12x13=(13+2) 10+6=150+6=156
ou (12+3)
10+6=156.
15x18=(18+5)
10+40=230+40=270
Se um dos factores é maior do que 20,
então procede-se de qualquer das maneiras seguintes: ou,
1.º se faz o produto de cada um dos
algarismos do multiplicando por 12, 13, 14, etc., escrevendo-se os
produtos da direita para a esquerda, assim:
634x12=7608
12x4=(4)8
12x3=36+4=(4)0
12x6=72+4=76
985x14=13790
14x5=(7)0
14x8=112+7=(11)9
14x9=126+11=137
2.º ou se multiplica o multiplicando por
10 e por 4 (se a multiplicação for 14, p. ex.) e se juntam, ou somam
os dois produtos. Exemplos:
645x14=6450+2580=9030
ou, 3.º se decompõe o mais pequeno em 2
factores — quando isso é possível — e se fazem os produtos,
sucessivamente, como em
675x14=675x7x2=4725x2=9450,
o que, quase
sempre, é possível e fácil.
No caso de um dos factores ser 15, pode,
ainda, proceder-se da seguinte forma: multiplica-se o multiplicando
por 10 e junta-se ao produto obtido mais metade deste, pois que
15=10+5.
Exemplo: 748x15=7480+3740=11220.
MULTIPLICAÇÃO POR 25
Sabido, como é, que 25=100/4, fácil se torna, a qualquer pessoa,
considerar o multiplicando multiplicado por 100, e achar-lhe a quarta
parte.
Exemplo: 6942x25= 694200/4=173550.
Claro que o mesmo produto se obterá, se
multiplicarmos 6942x5x5=34710x5=173550 visto que 25=5x5.
MULTIPLICAÇÃO POR 125
Este número,
125, é igual a 1000/8,
Logo, não teremos mais, para isso, do que
multiplicar o multiplicando por 1000, e, ao produto, achar-lhe um
oitavo. Assim, por exemplo:
888x125= 88888000/8=111000;
74856x125=9357000.
MULTIPLICAÇÃO POR 99,
999 9999. ETC.
Antes de mais nada, veja-se que 99=100-1;
999=1000-1 e 9999=10000-1. Sendo assim, significa isto que podemos
multiplicar o multiplicando por 100, 1000, 10000, etc., e subtrair, ao
produto, uma vez o multiplicando.
Exemplifique-se:
4686x99=468600-4686=463914
728x999=728000-728=727272; etc.
E não deixa de ser fácil, mesmo antes de
executar o produto, saber-se de quantos algarismos este há de constar:
compor-se-á de tantos, ou tantos menos um, quantos forem os algarismos
dos 2 factores, Ora veja-se:
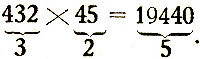 Mas isto quando? Mas isto quando?
Repare-se que os 2 algarismos da esquerda
— do multiplicando e do multiplicador — multiplicados entre si —16 —
dão um número de 2 algarismos, Quando isto acontece, o produto terá um
número de algarismos igual à soma dos dois, multiplicando e
multiplicador.
No caso contrário, isto é, de o produto
dele ser apenas de 1 algarismo, o produto terá tantos, menos um,
quantos os algarismos do multiplicando e do multiplicador, somados.
Além destas regras, e doutras idênticas,
inúmeras são aquelas que podem servir para abreviar a multiplicação,
bastando apenas um pouco de bom senso, e prática, que, evidentemente,
se impõem.
Suponhamos, agora, aplicado por exemplo às
fracções, o que acabamos de dizer, com respeito à multiplicação:
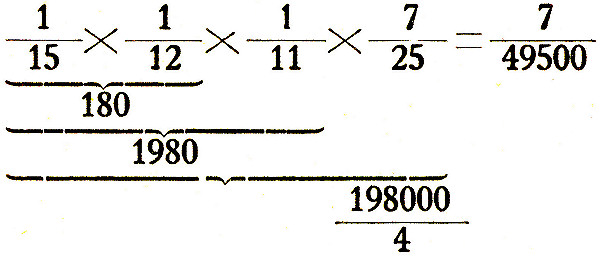

E, como estes, se resolvem todos os
produtos, de que aqui ficam apenas três fáceis exemplos.
Na
divisão
Por 10, 100, 1000, etc., de um número
inteiro.
a) ou ele termina em zero, ou zeros, e,
nesse caso, mais se não fará que eliminar um, dois, 3, etc. zeros; ou
b) termina em qualquer outro algarismo, e,
então, dividir-se-á por 10, 100, 1000, etc., contando, por meio de
vírgula, um, dois, 3 etc., dos algarismos da direita.
Exemplos:
Dividir o n.º 36000 por 10=3600;
por 100=360; por mil=36, e assim por
diante.
Dividir por 10, 100, 1000, etc. o número
128645.
a) por 10=12864,5
b) por 100=1286,45
c) por 1000=128,645, etc.
Divisão por
um n.º dígito: por 2, 3, 4, 5, etc.
Basta, para
isso, achar 1/3; 1/4; 1/5; 1/6, etc., desse número.
Exemplos: 93672/2=46836
93672/3=31224
93672/4=24418
93672/5=19534,4
DIVISÃO POR 25, 50,
75...
Por
25: Dividir um número por 25 é o mesmo que dividi-lo por 100, e
multiplicar, em seguida, o quociente por 4, visto que 25=100/4
Nestes termos,
18775:25=187,75x4=751
ou, porque
25=5x5, podemos dividir esse número por 5, e ainda o quociente
resultante novamente por 5. Assim,
134650:25=26930:5=5386
Por 50: Como 50= 100/2, o caso é
precisamente o mesmo que o antecedente: isto é, basta dividir o número
proposto — dividendo — por 100, e multiplicar o resultado por 2.
Exemplo:
6400:50=64x2=128
No
caso proposto, fica ainda campo para se praticar o que todos sabem já,
ou que
6400:50=640:5=128
Suponhamos, porém, que a simpatia do
cálculo nos leva para outra maneira de proceder, ou seja para aplicar
a decomposição em factores, visto que 50=2x5x5.
Nesse caso, 9720: 50=4860:25=972: 5=194,4 ou ainda 9720: 50=972:
5=194,4
Por
75: Sabido, como é, que 75=3/4x100, fácil é concluir que, para
executar a divisão de um número qualquer por 75, basta achar a terça
parte do resultado desse mesmo número dividido por 100, e multiplicar
o quociente resultante por 4.
Exemplo: 16824:75=56,08x4=224,32
Se pretendemos o quociente, obtido por
outro processo, praticamos como na divisão por 25, ou por 50, que o
caso é o mesmo, isto porque 75=3x25, ou 3x5x5, ou ainda 3x15. É, ainda
aqui, uma questão de simpatia. O resto... é uma brincadeira!
E vem agora a talhe de fouce dizer-se que,
sempre que o divisor é decomponível em factores, o cálculo mental, na
divisão, se torna simplicíssimo, sobretudo depois de se ter bem
praticado com a multiplicação, que é, como há muito se sabe, a
operação inversa da divisão.
DIVISÃO POR 125
Este número é a oitava parte de 1000. Então,
para se fazer a divisão de um número por 125, basta considerá-lo
dividido por 1000, e multiplicar o resultado por 8.
Exemplo: 12348:125= 12,348x8=98,784
Mas isto não quer dizer que não possamos,
ainda, como nos casos antecedentes, decompor 125 em 5x5x5, ou 5x25.
E não será preciso dizer mais, para se
concluir que o cálculo mental, sabidas meia dúzia de regras, não é mais
que uma brincadeira, por sinal de bom gosto. Pelo menos, eu assim o
entendo, e pratico, e não é de admirar, por conseguinte, que o exija,
pois o tenho por uma necessidade para a vida de todos os dias! |