|
I
Definição
de Lógica
Quantas
e quantas vezes, num quotidiano e rotineiro diálogo, produzimos uma
afirmação do género: o
teu ponto de vista peca por não apresentar lógica alguma.
Saber
o que é lógico, ou o que apresenta uma estrutura lógica , num
contexto linguístico, sempre foi uma questão de grande estudo e
reflexão, pelo menos desde a época da Revolução Socrática e seus
pensadores. Dentro destes, devemos destacar aquele que sem dúvida
mais contribuiu para o esclarecimento destas matérias, sendo ainda
considerado, nos nossos dias, uma referência incontornável devido ao
legado que nos foi transmitido.
Com
efeito, consideramos que os estudos de lógica clássica, ou formal,
foram na sua génese constituídos por essa grande figura da civilização
europeia que foi Aristóteles.
As
definições que hoje em dia apresentamos a respeito da Lógica,
enquanto ciência, fundam-se ainda no contributo do pensador de
Estagira.
Trata-se
de uma ciência que procura encontrar as leis em relação às quais o
nosso pensamento deve obedecer para que possa ser considerado válido.

Parece
confuso ? Então vamos por partes: como o pensamento produz raciocínios,
devemos pois analisar a essência ou estrutura do raciocínio para que
saibamos com exactidão do que é que falamos.
Dessa
forma, sabendo que os raciocínios,
ou argumentos, não são
mais do que um meio de passar de certos conhecimentos já adquiridos para outros,
que são as suas consequências, e apresentando-se esses conhecimentos
em juízos, ou proposições,
que , eles próprios,
religam ideias, designadas por conceitos
, ou termos, …surge daqui
a divisão tripartida da Lógica Formal:
- Lógica do Conceito,
Lógica do Juízo, Lógica do Raciocínio.
Maurice
Gex, Logique
Formelle,
pág. 17
II
O
problema da verdade material
e
da validade formal
Contrariamente
ao que se costuma pensar, a disciplina da lógica não se debruça
sobre a componente semântica dos conhecimentos expressos nos conceitos
ou nos juízos. A este respeito é costume efectuar uma distinção entre a
validade dos raciocínios
(saber se a conclusão está devidamente fundamentada nas informações
antecedentes - as premissas) e a verdade material
dos enunciados (saber se determinado enunciado é verdadeiro ou
falso, em confronto com a realidade empírica).
A
Lógica apenas irá debruçar-se sobre o primeiro caso, isto é,
averiguar se um determinado raciocínio chegou legitimamente a uma
conclusão, e nunca irá perder tempo em verificar se o raciocínio
assenta em pressupostos reais ou irreais.
Podemos
pois dizer que à lógica em nada interessa o problema da verdade.
É
pois possível produzirmos raciocínios válidos, mas assentes em
premissas (informações) falsas, e raciocínios inválidos, mas
assentes em verdades factuais, empiricamente verdadeiras.
Vejamos
um exemplo de um raciocínio válido, mas materialmente falso:
Se...
Todos os Homens são imortais
E
se... Todos
os batráquios são Homens
Logo,
Todos os batráquios são imortais
Com
efeito, logicamente é possível chegarmos a uma conclusão legítima,
na medida em que ela se encontra fundada nas premissas apresentadas,
independentemente do conteúdo veiculado.
Vejamos
agora um outro exemplo, nomeadamente de um raciocínio inválido, mas
que materialmente ou semanticamente é irrepreensível :
Todos
os Homens são mortais
Todos
os Homens são mamíferos
Todos
os mamíferos são mortais
Trata-se
de uma nítida infracção
às mais básicas regras da Lógica Formal. Podemos desde já, pelo
sentido, constatar que a informação dada nas premissas não permite
fundamentar a conclusão. Se referimos que todos os homens são
mortais e se todos os homens são mamíferos , a partir destas indicações,
jamais poderíamos justificar a conclusão de que todos os mamíferos
são mortais (quando muito poderíamos referir que alguns mamíferos são
mortais).
Apesar
de se estruturar unicamente em verdades materiais, sob um ponto de
vista lógico, o raciocínio não é válido.
III
O
conceito
Procuremos
relembrar os conteúdos estudados: O pensamento produz raciocínios
que conjugam juízos e
estes, por sua vez, efectuam relações entre conceitos.
Iremos
agora elucidar o significado de conceito.
Definição:
o conceito é uma representação mental que reúne numa
expressão linguística (termo), uma série de características comuns
a uma conjunto de seres. A partilha da mesma essência, permite a
estes elementos formarem uma mesma classe e serem designados pelo mesmo nome.
Exemplo:
o conceito de felino reúne numa palavra
todos os elementos e seres (gato, tigre, lince, puma, leão)
que partilham um conjunto de características genéricas (animal, ser
vivo, mamífero, vertebrado) e as diferenças específicas ( aquelas
características que só os felinos possuem e mais nenhuma outra
classe possui).
Quando
definimos um determinado conceito, poderemos consequentemente
distingui-lo de todos os restantes, em virtude da diferença
específica. Assim, quando nos referimos ao conceito cão e ao
conceito gato, a diferença específica de cada um destes
conceitos é inconfundível: o cão é um animal que ladra (diferença
específica) e gato é um animal que mia (diferença específica). As
características genéricas ajudam a definir o conceito, sob o ponto
de vista da compreensão e poderão ser comuns a diferentes conceitos
. No presente caso, o conceito de cão e o de gato têm em comum,
entre outras, as seguintes características: ser vivo, animal,
vertebrado, mamífero, animal com cauda...etc.

Apesar
das diferenças específicas, cão e gato partilham características
comuns ...
IV
O
Juízo
O
Juízo é uma operação mental que
une dois conceitos por meio de uma afirmação ou negação. Um dos
conceitos será o sujeito e o outro será o predicado. Na sua
estrutura clássica, o juízo apresenta ainda no início da sua
formulação um quantificador que
conjugado com o tipo de ligação existente entre os conceitos origina
uma das seguintes quatro possibilidades:
Todos
(quantificador)os gatos (conceito) são (ligação) felinos
(conceito).
Nenhum
(quantificador) gato(conceito) é (ligação) felino (conceito).
Alguns
(quantificador) gatos (conceito) são felinos (conceito)
Alguns
(quantificador) gatos (conceito) não são felinos (conceito)
V
O
Raciocínio
O
Raciocínio, como vimos no início, permite a passagem de
conhecimentos adquiridos para conhecimentos ainda não adquiridos.
Referimos também que esses conhecimentos se expressam em juízos e
que estes, por sua vez, unem dois conceitos.
Dessa
forma, considera-se que um raciocínio expresso numa inferência
mediata deverá conter dois conceitos e três juízos, sendo dois
deles considerados premissas, e o último deles, a conclusão.
Vejamos
um exemplo (como foi inicialmente referido, a componente da verdade
material nada interessa, pois perderíamos imenso tempo a verificar se
há ou não correspondência com a realidade. Para além deste
aspecto, certas verdades, ou mentiras, são muito polémicas. Senão
vejamos:
Todos
os portugueses (conceito) são admiradores de obras de arte
(conceito).
Todos
os adeptos do FCP (conceito) são portugueses (conceito)
Todos
os adeptos do FCP são admiradores de obras de arte.
Este
é um raciocínio inquestionavelmente válido, pois a conclusão
encontra-se fundamentada nas premissas. Isto é, o encadeamento das
duas primeiras premissas, ou juízos, permite a sustentação da
conclusão (3º juízo).
Se
não concordamos com a verdade material aqui expressa, poder-se-á
mudar o conceito FCP por um outro qualquer (SLB ou SCP), não devendo
ser um pretexto futebolístico que origine desconfianças em relação
à Lógica Aristotélica.
VI
Algumas
demonstrações matemáticas
A
matemática não é uma ciência experimental em que a repetição de
um fenómeno um grande número de vezes leva a aceitá-la como lei. O
conhecimento matemático é demonstrativo. Ora, os conhecimentos de Lógica
Formal são um pré-requisito para o estudo da matemática. Não
podemos esquecer que a Lógica é um instrumento ao serviço de
todas as ciências.
Vejamos
algumas demonstrações matemáticas, escolhidas do tema “sucessões”:
Demonstração
por dedução
Recorrendo
ao cálculo dedutivo, a partir de uma proposição deduz-se uma outra.
Exemplo:
Cálculo da soma dos n termos de uma progressão aritmética
Seja:
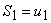
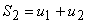
:
:
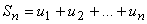 (1)
- representa a soma dos n primeiros termos de uma
progressão aritmética.
(1)
- representa a soma dos n primeiros termos de uma
progressão aritmética.
Por
outro lado, e uma vez que a adição é comutativa se trocarmos a
ordem dos termos a somar tem-se:
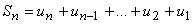 (2)
(2)
Adicionando
termo a termo as expressões (1) e (2),
obtém-se
(Numa
progressão aritmética, a soma dos termos igualmente distanciados dos
extremos é igual à soma dos extremos)
Logo,
|
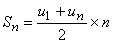
|
é
a soma dos n termos de uma progressão aritmética
|
Demonstração
por Indução
Demonstram-se casos
particulares, generalizando para todas as situações.
| Exemplo: prove por
indução matemática que: |
|
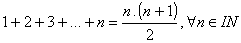 |
O
processo de demonstração por indução matemática apoia-se nos
passos seguintes:
1º
Provar a veracidade para n = 1
| Se n = 1,
vem |
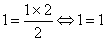 |
A propriedade é
verdadeira para n = 1
2º
Suponhamos que é verdadeira para p, ou seja
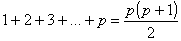 (1)
(1)
Vamos
provar que é válida para p + 1 , isto é
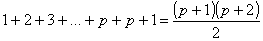 (2)
(2)
| Partindo de (1)
e adicionando |
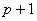 |
aos dois membros vem: |
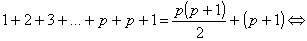
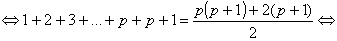
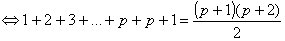 (2)
(2)
Concluímos então,
que se for verdadeira para o inteiro p, também é verdadeira
para
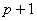
| Então ficou
demonstrado que |
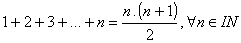 |
Demonstração
por Redução ao Absurdo
Demonstra-se
o teorema através de uma contradição, ou seja: para provar que o
teorema é verdadeiro, admitimos que a tese é falsa e através de um
raciocínio lógico, chega-se a uma contradição com a hipótese.
Pode-se assim concluir que a tese é verdadeira.
Exemplo:
Teorema da unicidade do limite
(uma
sucessão não pode tender para dois limites diferentes)
Demonstração:
Suponhamos que
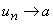 e
e
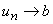 , com a <b
, com a <b
Então
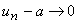 e
e
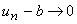
Seja
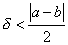 ( d
é um número menor do que metade da distância entre a e b
)
( d
é um número menor do que metade da distância entre a e b
)
| Existe uma ordem |
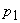 |
, a partir da qual |
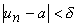 |
| Existe também uma
ordem |
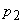 |
, a partir da qual |
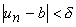 |
a - d
a a + d
b - d
b b + d


 Para
a maior das ordens Para
a maior das ordens
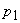 ou
ou
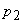 , os termos da sucessão
, os termos da sucessão
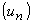 distam de a e de b
distam de a e de b
menos do que d,
o que é absurdo pois
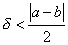 .
.
O absurdo resulta de
se ter considerado
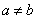 .
.
Logo
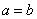 .
.
Bibliografia:
NEVES, Maria Augusta
Ferreira, Matemática, 11º
ano, Parte 3, Porto Editora. 1998.
|