Núcleo de Estágio de Matemática 2002/03

Conhecemos a parábola como gráfico de uma função quadrática. A parábolas intervêm no estudo de problemas do âmbito da Astronomia, da Física e de outras ciências, como por exemplo, o estudo do lançamento de projécteis.

Na Antiguidade a parábola a parábola foi definida como uma secção cónica (tal como a elipse): cortando uma superfície cónica segundo um plano paralelo a uma das geratrizes obtém-se uma parábola. (vd. Infinito 10.º ano, vol. II, pág. 254)

Como lugar geométrico, a parábola é o conjunto dos pontos do plano equidistantes de uma recta – directriz- e de um ponto que não lhe pertence – foco.

O foco da parábola goza das seguintes propriedades:

1. Todo o raio luminoso que incide num espelho parabólico, paralelo ao eixo da parábola, reflecte-se passando pelo foco.

2. Todo o raio luminoso que incide no espelho parabólico passando pelo foco reflecte-se paralelamente ao eixo.

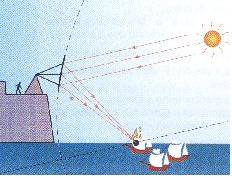
Estas propriedades são conhecidas desde o século III a. C.: durante o cerco de Siracusa, Arquimedes inventou uma forma de incendiar barcos romanos, usando espelhos parabólicos, os “ustórios”. Estes espelhos faziam convergir os raios solares reflectidos sobre os barcos, incendiando-os. 

Nos nossos dias as superfícies parabólicas, geradas pela rotação de uma parábola em torno do seu eixo, têm várias aplicações:  por exemplo, as antenas parabólicas de televisão e os radiotelescópios, cujo funcionamento é justificado pela primeira propriedade. A segunda propriedade aplica-se aos projectores tais como os faróis dos automóveis.