|
Soluções
|
|
Problema 1
|
|
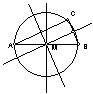
Construindo
as mediatrizes dos lados do triângulo, verificamos
que estas se intersectam no ponto médio da
hipotenusa. Assim, num triângulo rectângulo, o
circuncentro é o ponto médio da hipotenusa.
|
|
|
De
facto, o ponto C pertence à circunferência de diâmetro
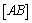 ,
pois esta circunferência é o lugar geométrico dos
pontos P tais que
,
pois esta circunferência é o lugar geométrico dos
pontos P tais que
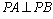 (ângulos
inscritos numa semi-circunferência).
(ângulos
inscritos numa semi-circunferência). |
|
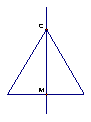 |
Num
triângulo equilátero as alturas e as medianas
coincidem e estão contidas nas mediatrizes, logo
intersectam-se no mesmo ponto e, portanto, o
ortocentro, o baricentro e o circuncentro são
coincidentes. |
|
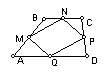
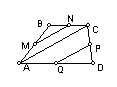
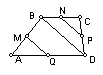
Unindo
com segmentos de recta os pontos médios dos lados
de um qualquer quadrilátero obtém-se um
paralelogramo. |
|
Este
resultado pode ser facilmente demonstrado,
recorrendo a vectores e às propriedades das operações
entre vectores. |
|
|
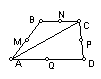
Provemos
que
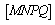 é um
paralelogramo.
é um
paralelogramo.
Consideremos
os
vectores 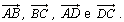
|
|
|
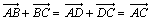
Temos
que 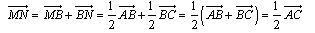
|
|
e,
por outro lado,
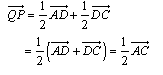
|
|
|
Então,
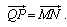
De forma
análoga, considerando que 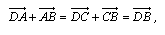
se
mostra que 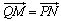
|
|
Podemos
então concluir que os lados opostos do
quadrilátero 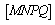 são iguais e paralelos, pelo que
são iguais e paralelos, pelo que 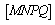 é um paralelogramo.
é um paralelogramo. |
|
|
|
|
|
Se
o aventureiro efectuou o deslocamento descrito chegou ao
ponto inicial, então teria que se encontrar no Pólo
Norte, logo o urso era branco. |

|
|