|
Pontos
notáveis de um triângulo
|
1.
O incentro
Chama-se
bissectriz de um ângulo à recta que divide o ângulo
em duas partes iguais. Ao ponto de intersecção das
bissectrizes dos ângulos de um triângulo chamamos
incentro. Este ponto é o centro da circunferência
inscrita no triângulo.
|
|
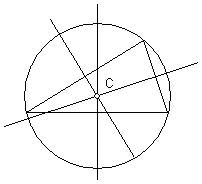
Com
os três vértices do triângulo pode-se traçar um
circunferência na qual o triângulo fica inscrito.
O centro desta circunferência é o circuncentro -
ponto de intersecção das mediatrizes dos lados do
triângulo. |
 |
|
3.
O baricentro |
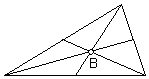 |
Unindo
o ponto médio de cada lado do triângulo ao vértice
oposto obtém-se um segmento de recta designado mediana.
O ponto onde se intersectam as medianas é o
baricentro ou centro de gravidade do triângulo. |
|
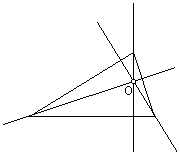
O
ortocentro é o ponto onde se intersectam as alturas
do triângulo, isto é, as perpendiculares traçadas
desde os vértices até aos lados opostos (ou seus
prolongamentos). |
 |
A
linha de Euler
|
 |
Leonhard
Euler (1707-1783) foi um matemático que se dedicou,
entre outros ramos, à geometria. Um dos seus
resultados mais curiosos é o facto de que, para
qualquer triângulo, o circuncentro, o baricentro e
o ortocentro estão sobre a mesma linha recta: a
linha de Euler. |
Actuais
programas de geometria dinâmica, por exemplo o Geometer’s
Sketchpad, permitem confirmar este facto.
|