|
1
Era
dado o cubo de vértices A, B, C, D, E, F, G, H,
representado na figura e pedia-se para provar que o sólido
definido pelos vértices A, C, F, H é um tetraedro
regular.
Ora
as arestas [AC], [CF], [FH] e [AF] são diagonais faciais
do cubo, logo os triângulos (as faces do tetraedro) [ACF],
[AFH], [CFH] e [ACH] são iguais. Por outro lado, em cada
um dos vértices concorrem sempre três faces. Portanto, o
sólido é um sólido regular constituído por quatro triângulos,
logo é um tetraedro.
2
a)
Era
dada a figura e pedia-se para provar que a pirâmide
de base IJK e de vértice F, que está
contida no tetraedro sombreado, é um tetraedro regular.
Observe-se que o triângulo [IJK] é semelhante ao triângulo
[BEG], de razão de semelhança
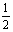, uma vez que I,
J e K são ao pontos médios de [EG], [EB] e [BG],
respectivamente.
Sendo
d a medida do comprimento da diagonal facial do
cubo, cada uma das arestas do tetraedro mede
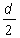. (Note-se que,
por exemplo, I é também o ponto médio de [HF],
logo
.)
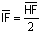De forma análoga à alínea anterior se conclui
que a pirâmide é um tetraedro.
Era
também pedida a relação entre o volume deste pequeno
tetraedro e o volume do tetraedro sombreado.
Já
foi referido que os triângulos que constituem as faces do
pequeno triângulo e os das faces do tetraedro sombreado são
semelhantes e têm razão de semelhança
.
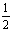Então
a razão entre os volumes é
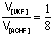, ou seja,
.
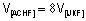b)
Observe-se que os vértices da stella octangula são
os vértices do cubo. Assim, escolhendo um referencial o.
m. em que a origem coincide com o vértice D, e em que os
eixos Ox, Oy e Oz são definidos pelas rectas DA, DC e DH,
respectivamente, as coordenadas dos vértices são: A(a,0,0),
B(a,a,0),
C(0,a,0),
D(0,0,0), E(a,0,a),
F(a,a,a),
G(0,a,a)
e H(0,0,a),
onde a
é a medida do comprimento da aresta do cubo.
c)
Nesta alínea pedia-se a percentagem do cubo que é
ocupada pela stella octangula.
Considere-se
o cubo e o tetraedro sombreado nele inscrito. Além do
tetraedro, podem-se ainda “encaixar” no cubo quatro
pirâmides triangulares rectas congruentes com a pirâmide
[ABDH] e cujo volume é
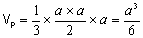
Então,
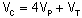, ou seja,
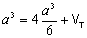, logo o volume do tetraedro sombreado é
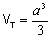, onde a
é a medida do comprimento da aresta do cubo.
Por
outro lado,
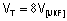, logo
.
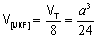Como
a stella octangula é constituída pelo tetraedro
sombreado e por quatro pequenos tetraedros brancos
congruentes com o tetraedro [IJKF]
, então o seu volume é
.
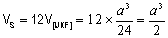Daqui
se conclui que a stella octangula ocupa 50% do
cubo.
|
|
Partindo
do princípio de que as toupeiras mentem, os outros
agentes dizem a verdade, perguntou-se:
1.
Se só há uma toupeira entre os três, quem é ela?
2.
Se há duas toupeiras presentes, quem são elas?
Ao
afirmar “O Júlio está a mentir”, O Célio esta a
dizer que “O Célio não é uma toupeira.”
Vamos
representar por J a proposição “O Júlio é uma
toupeira” e por C a afirmação “o Célio é uma
toupeira”.
Assim,
dos interrogatórios realizados resultaram os seguintes
testemunhos:
Alberto:
J ;
Júlio: C
;
Célio: ~C
~C
é a negação de C, por isso uma e uma só destas duas
proposições é verdadeira.
1.
Se apenas uma pessoa mente então a proposição J é
verdadeira, isto é, o Júlio é a toupeira.
2.
Se duas pessoas mentem, então a proposição J é falsa,
por isso o Júlio não é uma toupeira. Além disso, pode
concluir-se que Alberto é uma toupeira, pois mentiu no
interrogatório.
Então
as toupeiras são o Alberto e o Célio.
|
