|

|
|
Núcleo
de Estágio de Matemática 2002/03 |
|
|
|
|

|
Escola
Secundária José Estêvão
Folha de
Matemática n.º 1
Dezembro de 2002 |
|
|
|
Desafios
|
|
Problema 1
|
|
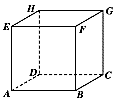
Considere
o cubo de vértices A, B, C, D, E, F, G, H,
representado na figura.
|
|
|
1 - O sólido definido
pelos vértices A, C, F, H é um tetraedro regular.
Porquê?
2
- Os
restantes quatro vértices do cubo (B, D, E e G)
definem outro tetraedro. A combinação destes dois
tetraedros forma uma stella octangula.
|
|
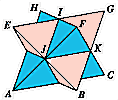
a)
- Um dos tetraedros que a compõem está
sombreado. A pirâmide de base IJK e de vértice
F, que está contida no tetraedro sombreado,
é um tetraedro regular. Porquê? |
|
|
|
Qual
é a relação entre o volume deste pequeno tetraedro e o
volume do tetraedro de cor? b)
- Situe
o cubo [ABCDEFGH] num referencial cartesiano conveniente e
indique as coordenadas dos vértices da stella
octangula.
c)
- Que percentagem do cubo é ocupado pela stella
octangula)?
|
|
|
|
Problema 2
|
|
|
Três
espiões, suspeitos de serem agentes duplos, disseram o
seguinte quando foram interrogados:
|
|
Alberto:
O Júlio é uma toupeira.
Júlio:
O Célio é uma toupeira.
Célio:
O Júlio está a mentir. |

|
|
|
1
- Partindo
do princípio de que as toupeiras mentem, os outros
agentes dizem a verdade e só há uma toupeira entre os três,
quem é ela?
2
- Se, por outro lado, há duas toupeiras
presentes, quem são elas?
|
|
|
|
|
|
|
|
|
|
|