|

|
|
Núcleo
de Estágio de Matemática 2002/03 |
|
|
|
|

|
Escola
Secundária José Estêvão
Folha de
Matemática n.º 0
Novembro de 2002 |
|
|
|
Desafios
|
|
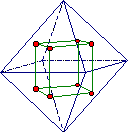
Problema 1
Unindo os
centros das faces consecutivas de um poliedro convexo
obtemos o seu dual.
Considera
o octaedro e o seu dual representados na figura. Se a
aresta do octaedro medir 12 cm quanto mede a aresta do
cubo?
|
|
Convidamos-te
a apresentar uma resolução deste problema a um
professor de Matemática desta escola. |
|
|
Quadrados Mágicos
|
|
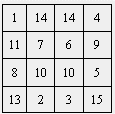
Este
quadrado pode ser visto na Igreja da Sagrada Família,
em Barcelona. Este monumento foi projectado por Gaudí,
a sua construção foi iniciada em 1883 e ainda
decorre. |
 |
|
|
|
O
que é um quadrado mágico?
Um
quadrado mágico de ordem n é uma tabela com
n linhas e n colunas, preenchida com números
inteiros, de forma a que a soma dos n números
de cada linha, coluna ou diagonal seja sempre
o mesmo número. A este número dá-se o nome
de constante mágica.
|
|
|
|
|
O
quadrado apresentado é um quadrado mágico de ordem 3 com
constante mágica 33. Terá a constante mágica algum
significado especial? Qual?
|
|
|
Problema 2
|
|
Construa
um quadrado mágico de ordem 3 com os números 1, 2, 3, 4,
5, 6, 7, 8 e 9.
|
|
|
|
|
|
|