![]()
Uma caixa de sapatos é um bom modelo de um
paralelepípedo rectângulo. 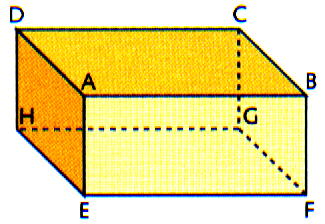 O paralelepípedo rectângulo tem:
O paralelepípedo rectângulo tem:
6 faces rectangulares. 8 vértices: A, B, C, D, E, F, G, H. 12 arestas: [AB], [BC], [CD], [DA], [EF], [FG], [GH], [HE], [AE], [BF], [CG] e [DH] Além disso: As faces que se intersectam estão contidas em planos perpendiculares. As faces opostas estão contidas em planos paralelos. Dois vértices que não pertençam à mesma face dizem-se opostos. - São opostos:{(A, G), (B, H), (C, E), (D, F)}. - Não são opostos, por exemplo: (A, C), uma vez que pertencem à mesma face, [ABCD]. (A, F), uma vez que pertencem à mesma face, [AEFB]. O segmento de recta que une dois vértices opostos de um paralelepípedo rectângulo denomina-se diagonal. Então, [AG], [BH], [CE] e [DF] são diagonais.
Vamos aplicar o teorema de Pitágoras para determinar a medida da diagonal de um paralelepípedo rectângulo de dimensões a, b e c. Como classificarias o triângulo [EFG]?
Podes ter algumas dúvidas, porque a figura está construída de modo a dar a ideia de espaço tridimensional e o rectângulo [EFGH] está deformado. Mas ele é realmente um rectângulo e [EFG] é um triângulo rectângulo em F. A que será igual a medida de [EG] (designada por x na figura)? Para saberes, clica na palavra RESOLUÇÃO. |